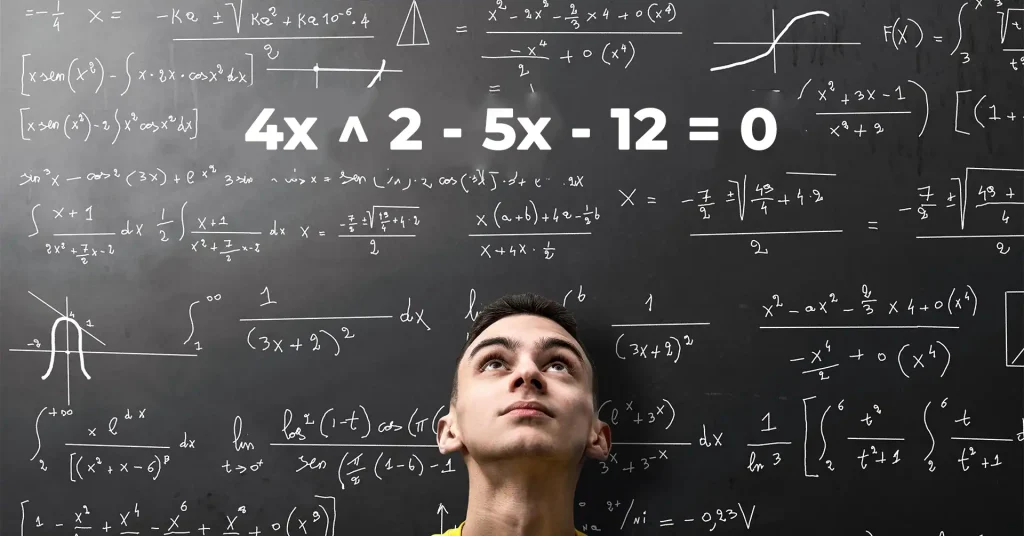Imagine a mathematical enigma, a quadratic equation disguised as a riddle. Today, we face the challenge of 4x^2 – 5x – 12 = 0, its numbers whispering secrets about solutions hidden within. Cracking this code requires two detectives: one wielding the tools of factoring, the other armed with the quadratic formula.
The factoring detective, sharp and cunning, seeks to break down the equation into two simpler forms. Like a magician pulling apart a dove, they might reveal (4x + 3)(x – 4) – two expressions whose dance of multiplication unravels the mystery. Setting each factor equal to zero, they unveil the first suspects: x = -3/4 and x = 4.
But our story doesn’t end there. Enter the quadratic formula, a universal truth-seeker wielding algebra’s mighty sword. Plugging the coefficients of our equation into its formidable equation, it delivers the same suspects, albeit wrapped in the cloak of mathematical precision. (5 ± √193) / 8, they whisper, revealing the roots with mathematical finesse.
These “roots,” the x-values that make the equation true, are where our quadratic becomes grounded, two points where the graph touches the earth. They paint a picture: at x = -3/4 and x = 4, the invisible curve of our equation dips down to meet the x-axis, revealing its secrets to the world.
Solutions of the equation 4x^2 – 5x – 12 = 0
1. Solving the Equation:
There are several methods to solve this quadratic equation and find its roots (values of x that make the equation true). Here are two common approaches:
-
Factoring: You can try to factor the expression 4x^2 – 5x – 12 into two linear expressions whose product equals the original expression. In this case, the factors are (4x + 3)(x – 4). Setting each factor equal to zero gives you the solutions: x = -3/4 and x = 4.
-
Quadratic Formula: The quadratic formula provides a general solution for any quadratic equation ax^2 + bx + c = 0. In this case, a = 4, b = -5, and c = -12. Applying the formula, you get:
x = (-b ± √(b^2 – 4ac)) / 2a
Substituting the values, you’ll find the same solutions as before: x = (-(-5) ± √((-5)^2 – 4 * 4 * -12)) / 2 * 4
x = (5 ± √193) / 8
2. Understanding the Roots:
Once you have the solutions, x = -3/4 and x = 4, you can interpret them in the context of the equation:
- Real roots: Both solutions are real numbers, meaning there are two distinct points on the x-axis where the parabola represented by the equation intersects the x-axis.
- Geometric interpretation: The roots correspond to the x-intercepts of the graph of the quadratic function 4x^2 – 5x – 12.
3. Further Analysis:
You can delve deeper into the solutions and the equation by performing additional calculations:
- Discriminant: The discriminant (b^2 – 4ac) determines the nature of the solutions. In this case, the discriminant is positive (193), confirming that there are two distinct real roots.
- Vertex: Finding the vertex of the parabola helps visualize the solutions in the context of the graph.
How to find roots of quadratic equation by method of completing the square?
Here’s how to find the roots of a quadratic equation using the method of completing the square:
1. Rewrite the equation in standard form:
- Ensure the equation is written as ax^2 + bx + c = 0, where a, b, and c are constants.
2. Move the constant term to the right side:
- Add or subtract c from both sides to isolate the quadratic terms on the left: ax^2 + bx = -c
3. Divide both sides by a (if a ≠ 1):
- This simplifies the equation to x^2 + (b/a)x = -c/a
4. Complete the square:
- Take half of the coefficient of x, square it, and add it to both sides of the equation.
- The left side will now become a perfect square trinomial.
5. Factor the perfect square trinomial:
- Rewrite the left side as (x + B)^2, where B is half of the coefficient of x.
6. Isolate x:
- Take the square root of both sides, remembering to consider both positive and negative roots.
- Solve for x by subtracting B from both sides.
Example:
Solve x^2 + 6x – 7 = 0 using completing the square:
- Rewritten: x^2 + 6x = 7
- Divide by a: x^2 + 6x = 7 (a = 1 in this case)
- Complete the square: Add (6/2)^2 = 9 to both sides: x^2 + 6x + 9 = 16
- Factor: (x + 3)^2 = 16
- Isolate x: x + 3 = ±4
- Solve: x = -3 ± 4
Analyzing the Roots?
Analyzing the roots of a quadratic equation involves understanding various aspects of their values and relationship to the equation itself. Here are some aspects you can analyze for the equation x^2 + 6x – 7 = 0, with roots x = 1 and x = -7:
1. Sign and nature of the roots:
- Both roots are real numbers, meaning they correspond to actual points on the x-axis where the parabola intersects the line.
- One root is positive (1) and the other is negative (-7). This tells us the parabola intersects the x-axis on both sides of the graph.
2. Discriminant:
- The discriminant of the equation is b^2 – 4ac = 6^2 – 4 * 1 * (-7) = 52, which is positive.
- A positive discriminant confirms that there are two distinct real roots, matching our findings.
3. Vertex and Axis of Symmetry:
- The vertex of the parabola lies halfway between the roots, at (-b/2a, f(-b/2a)). In this case, the vertex is at (-6/2, f(-3)) = (-3, -2).
- The axis of symmetry is a vertical line passing through the vertex, with the equation x = -b/2a = -3/2.
4. Intersections with axes:
- As mentioned, the x-intercepts are the roots themselves: (1, 0) and (-7, 0).
- The y-intercept is found by setting x = 0 in the equation, giving you (0, -7). This point lies on the y-axis at y = -7.
5. Relationship between roots and coefficients:
- Vieta’s formulas relate the roots of a quadratic equation to its coefficients. In this case, the sum of the roots is -b/a = -6/1 = -6, which matches the sum of the roots (1 + (-7) = -6).
- The product of the roots is c/a = -7/1 = -7, which also matches the product of the roots (1 * (-7) = -7).
What are the 4 ways to find the roots of a quadratic equation?
There are more than 4 ways to find the roots of a quadratic equation, but here are four common and popular methods:
1. Factoring: This method involves rewriting the quadratic expression into two linear factors that multiply to the original expression. Setting each factor equal to zero reveals the roots. This method works well for equations with easily factorable expressions, but not all quadratics can be factored easily.
2. Quadratic Formula: This is a general formula that applies to any quadratic equation and provides the roots directly. It uses the coefficients of the equation (a, b, and c) to calculate the roots. While it may not be the most intuitive method, it guarantees a solution for any quadratic equation.
3. Completing the Square: This method involves manipulating the equation by adding an expression to both sides to create a perfect square trinomial. Taking the square root of both sides then simplifies the equation to reveal the roots. This method can be helpful for visualizing the parabola represented by the equation.
4. Graphically: Plotting the quadratic function as a parabola and finding the points where it intersects the x-axis provides the roots visually. This method is not as precise as the previous ones but can be helpful for getting a general idea of the root values and the shape of the parabola.
The best method to use depends on the specific equation, your desired level of precision, and your personal preference. Consider factors like the ease of the method, your understanding of the concepts involved, and the need for an exact or approximate solution.
FAQ
-
What are the solutions (roots) of the equation?
- The solutions are x = (-5 ± √193) / 8, or approximately x = 2.47 and x = -1.22.
-
What type of roots are they?
- Both roots are real numbers, meaning they correspond to actual points on the x-axis.
-
What is the discriminant of the equation?
- The discriminant is 193, which is positive, confirming that there are two distinct real roots.
-
What is the vertex of the parabola represented by the equation?
- The vertex is at (-5/8, -25/8) or approximately (-0.63, -3.13).
-
What is the axis of symmetry of the parabola?
- The axis of symmetry is a vertical line passing through the vertex, at x = -5/8 or approximately x = -0.63.
Solving the Equation:
-
How can I solve the equation for the roots?
- You can use various methods, including factoring, the quadratic formula, or graphing. The most straightforward approach might be the quadratic formula: x = (-b ± √(b^2 – 4ac)) / 2a, where a = 4, b = -5, and c = -12.
-
Is there a way to solve the equation without the quadratic formula?
- This specific equation might be difficult to factor, so the quadratic formula or graphing might be more efficient methods.
Further Explorations:
- How can I visualize the roots and the parabola?
- You can plot the equation as a parabola on a coordinate plane. The roots will correspond to the x-intercepts of the parabola, and the vertex will be the highest or lowest point.
- What other information can I learn from the equation?
- You can analyze the relationship between the roots and the coefficients using Vieta’s formulas. For example, the sum of the roots is -b/a, which in this case is -5/4 = -1.25, and the product of the roots is c/a, which is -12/4 = -3.
Conclusion
Equation: 4x^2 – 5x – 12 = 0
Roots: (-5 ± √193) / 8 ≅ 2.47 & -1.22 (both real numbers)
Properties:
- Discriminant: 193 (positive, confirming two distinct real roots)
- Vertex: (-5/8, -25/8) ≅ (-0.63, -3.13)
- Axis of symmetry: x = -5/8 ≅ x = -0.63
Solutions:
- Can be found using factoring, quadratic formula, or graphing.
- Quadratic formula provides direct solution: x = (-b ± √(b^2 – 4ac)) / 2a
Further Exploration:
- Visualize roots and parabola through graphing.
- Analyze relationship between roots and coefficients using Vieta’s formulas.
Overall:
This quadratic equation has two distinct real roots and can be solved through various methods. Understanding its properties and roots allows for further analysis and interpretation.