Triangles have a special role in the field of geometric figures since they are the starting point for closed shapes created by straight lines. Since no closed structure can be formed by two straight lines, we’ll need three straight lines to make this shape, and because of its rarity, knowledge of measurements like area of triangle and its perimeter become essential in the real world.
There are three sides of a triangle, and they converge at three distinct points. We may change the length of the triangle’s sides and the angle they form with each other in an infinite number of ways, resulting in a vast number of different forms of triangles.
Several triangles have symmetry in their form, and these triangles are grouped as equilateral triangles, isosceles triangles, and right-angled triangles, although there are also other triangles in general. Let’s take a look at how we find the perimeter of a triangle and the area of a triangle.
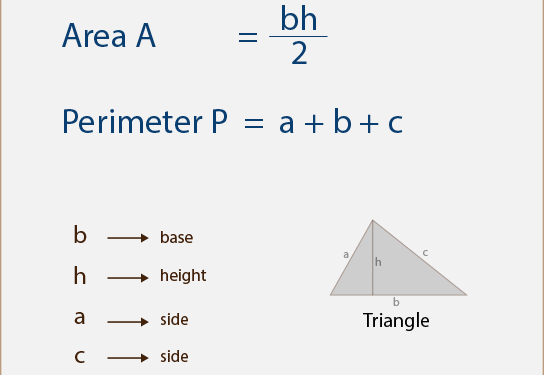
The perimeter of any geometric figure is the path around its boundary. In the case of a triangle, the length of the periphery is equal to the sum of the length of its three sides . Now, if it is an equilateral triangle, it’ll be straightforward since the three of the sides will be of the same length, so if the side dimension is ‘a’ the perimeter will be 3a.
If the lengths of the sides of a triangle are a, b, and c, the perimeter of the triangle will be a + b + c.
Before dealing with the triangles, it should be kept in mind that triangles and trigonometry are inextricably linked. In triangles, trigonometry is commonly used to calculate the missing length of the side and the missing angle value. To calculate triangles area we use the following formula also called the Heron formula:
The area of a triangle with three known sides is equal to the square root of [s (s-a) (s-b) (s-c)].
Where “s” is the semi-perimeter of the triangle, which is s = (a + b + c) / 2, where a, b, and c are the lengths of the triangle’s edges.
So, if the lengths of the triangle’s sides are known, the area of the triangle can be calculated using Heron’s formula and the triangle’s semi-perimeter.
The formula for special triangles, on the other hand, can be generalized due to the special properties of such special triangles. Let’s say you have an equilateral triangle with the length of one side equal to y. Let us see how to find its area now.
Again we apply Heron’s formula and find the semi perimeter, which will be 3y/2
Area of this equilateral triangle = square root of s(s-y)3
S – y = 3y/2 – y = y/2
The square root of s(s-y)3 = square root of (3y/2 * y3/8)
= square root of (3y4/16)
= (square root of 3) * (y2/4)
Now, if we have an isosceles triangle whose base and height is known, then the area of the triangle is = 1/2 ( Base * Height)
Also, note that the area of a triangle is expressed in square units.
Because of the ubiquitous use of triangular shapes in daily life, the area and perimeter of a triangle are among the most frequently measured scales. The ease with which the area and diameter of triangles can be measured, particularly for equilateral triangles, makes it a useful shape to use.
Triangles problems can be practiced further using math worksheets that are freely accessible on the internet. Cuemath is one such website where students can find a range of geometry worksheets to help them develop their geometry skills.